Pengertian Invers Matriks
- Matriks bujur sangkar A dikatakan memiliki invers, jika terdapat matriks B sedemikan rupa sehingga : AB = BA = I, di mana I merupakan matriks identitas
- B dikatakan invers matriks A ditulis A^-1, maka AA^-1 = A^-1A = I
- A dikatakan invers matrik B ditulis B^-1, maka B^-1B = BB^-1
- Contoh ; AB = BA = I
Teknik Menghitung Matriks :
- Metode Adjoint Matriks
- Metode Operasi Elementer Baris
- Metode Perkalian Invers Matriks Elementer
- Metode Partisi Matriks
- Program Komputer - MATCADS, MATLAB
- WS OFFICE EXCELL
Andaikan A merupakan matriks bujur sangkar berordo (n x n), Cij = (-1)i + 1 Mij kofaktor elemen matriks aij dan andaikan pula det(A) != 0 (!= merupakan "bukan sama dengan"), maka A memiliki invers yaitu :
Kasus : n = 3, maka
Metode Perkalian Matriks Elementer
Matriks elementer adalah matriks yang diperoleh dari operasi elementer yang dikenakan pada matriks identitas. Setiap matriks elementer memiliki invers dan setiap matriks bujur sangkar berordo (n x n) yang memiliki invers ekivalen baris terhadap matriks identitas I. Akibatnya, jika :
Matriks elementer E diperoleh dari transformasi matriks identitas di mana pada kolom ke-I diganti dengan normalitas vektor kolom :
Di mana nilai Nki adalah
CONTOH
Metode Partisi Matriks
Partisi matriks A yang berordo (m x n) adalah sub matriks - sub matriks yang diperoleh dari A dengan cara memberikan batasan-batasan garis horizontal di antara dua baris dan atau memberikan batasan - batasan garis vertikal di antara dua kolom.
CONTOH
Andaikan A matriks bujur sangkar berordo (n x n) yang memiliki invers, yaitu : A^-1 = B dan partisinya masing-masing adalah :
Dari perkalian matriks diperoleh hasil :
Maka rumus untuk menghitung invers matriknya adalah :
Invers Matriks dengan metode partisi matriks
Contoh :

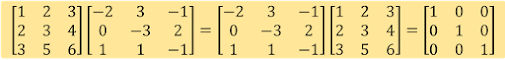




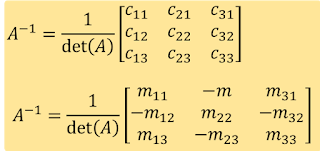





















Tidak ada komentar:
Posting Komentar