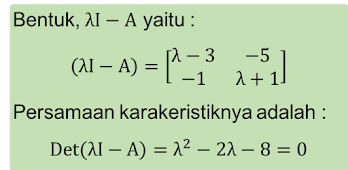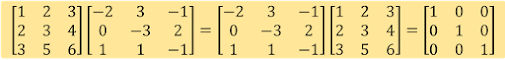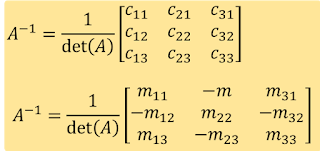Nilai Eigen Dan Vektor Eigen

Andaikan A matriks bujur sangkar berordo n x n, vektor taknol x di dalam R^n dikatakan vektor egien A, jika terdapat skalar taknol (lamda) sedemikian rupa sehingga,

lamda disebut dengan nilai eigen dari A dan x disebut vektor eigen dari A yang bersesuaian dengan lamda.

CONTOH :

Vektor x = [1, 2] adalah vektor eigen dari :

yang bersesuaian dengan nilai eigen, lamda = 3, karena :

Teknik Menghitung Nilai Eigen (1)

Untuk menghitung nilai eigen matriks A yang berordo n x n tulislah Ax = lamda x sebagai,

Agar lamda menjadi nilai eigen, maka penyeselaian sistem persamaan linear di atas harus non trivial, di mana syaratnya adalah :

Teknik Menghitung Nilai Eigen (2)

Persamaan terakhir adalah polinomial lamda berderajad n yang disebut dengan persamaan karakteristik A, sedangkan nilai eigen matriks A adalah akar-akar persamaan karakteristik A (Akar-akar polinomial dalam lamda).

Beberapa langkah untuk menentukan nilai eigen dan vektor eigen mariks A adalah :

1.  Bentuk matriks 

2.  Hitung determinan,

3.  Tentukan persamaan karakteristik dari,

4. Hitung akar-akar persamaan karakteristik (nilai lamda)

5.  Hitung vektor eigen dari SPL,

CONTOH :

Carilah nilai eigen dan vektor eigen dari ,

Jawab :

Akar-akar persamaan karakteristiknya adalah :

Vektor eigen x dari A diperoleh dari :

Jadi vektor eigen untuk lamda yang bernilai 4 adalah x = [5, 1]. Sedangkan vektor eigen untuk lamda yang bernilai -2 adalah x = [1, -1].

Sistem Persamaan Linear

Pengertian Sistem Persamaan Linear

Persamaan linear adalah suatu persamaan dengan n variabel yang tidak diketahui x1, x2, x3, ... , xn yang dinyatakan dalam bentuk :

dimana a1, a2, ..., an dan b adalah konstanta real (kompleks). Persamaan linear secara geometri dengan istilah garis.

CONTOH

Persamaan linear :

Secara umum, sistem persamaan linear adalah suatu susunan yang terdiri dari m persamaan linear dan n variabel yang tidak diketahui yang berbentuk :

dimana x1, x2, ..., xn disebut variabel yang tidak diketahui, aij konstanta koefisien sistem persamaan linear dan bj konstanta yang diketahui.

Bentuk Matriks SPL

Dalam bentuk matriks SPL dituliskan menjadi, AX = B, atau :

SPL, AX = B diklasifikasikan menjadi :

• SPL homogen, jika koefisien matriks B = 0
• SPL non-homogen, jika terdapat koefisien matriks B bukan nol

CONTOH :

SPL non-homogen

Bentuk Matriks SPL

Metode Crammer

Andaikan AX = B adalah sistem persamaan linear dengan n persamaan linear dan n variabel yang tidak diketahui

Andaikan determinan matriks A tidak sama dengan nol maka sistem persamaan linear non-homogen solusinya tunggal, yaitu

Di mana Di = det (Ai ) determinan matriks berordo (n x n) yang diperoleh dari A dengan cara mengganti kolom ke-i dengan koefisien matriks B

CONTOH : 

Carilah solusi SPL berikut dengan metode Crammer :

Jawab :

Bentuk matriks SPL, AX = B adalah :

Aljabar Lienar Invers Matriks

 

Pengertian Invers Matriks

• Matriks  bujur sangkar A dikatakan memiliki invers, jika terdapat matriks B sedemikan rupa sehingga : AB = BA = I, di mana I merupakan matriks identitas
• B dikatakan invers matriks A ditulis A^-1, maka AA^-1 = A^-1A = I
• A dikatakan invers matrik B ditulis B^-1, maka B^-1B = BB^-1
• Contoh ; AB = BA = I

Teknik Menghitung Matriks :

• Metode Adjoint Matriks
• Metode Operasi Elementer Baris
• Metode Perkalian Invers Matriks Elementer
• Metode Partisi Matriks
• Program Komputer - MATCADS, MATLAB
• WS OFFICE EXCELL

Metode Adjoint Matriks

Andaikan A merupakan matriks bujur sangkar berordo (n x n), Cij = (-1)i + 1 Mij kofaktor elemen matriks aij dan andaikan pula det(A) != 0 (!= merupakan "bukan sama dengan"), maka A memiliki invers yaitu :

dimana adj,

Kasus : n = 2, maka

Kasus : n = 3, maka

Metode Perkalian Matriks Elementer

Matriks elementer adalah matriks yang diperoleh dari operasi elementer yang dikenakan pada matriks identitas. Setiap matriks elementer memiliki invers dan setiap matriks bujur sangkar berordo (n x n) yang memiliki invers ekivalen baris terhadap matriks identitas I. Akibatnya, jika :

Matriks elementer E diperoleh dari transformasi matriks identitas di mana pada kolom ke-I diganti dengan  normalitas vektor kolom :

Di mana nilai Nki adalah

CONTOH

Metode Partisi Matriks

Partisi matriks A yang berordo (m x n) adalah sub matriks - sub matriks yang diperoleh dari A dengan cara memberikan batasan-batasan garis horizontal di antara dua baris dan atau memberikan batasan - batasan garis vertikal di antara dua kolom.

CONTOH

Andaikan A matriks bujur sangkar berordo (n x n) yang memiliki invers, yaitu : A^-1 = B dan partisinya masing-masing adalah :

Dari perkalian matriks diperoleh hasil :

Maka rumus untuk menghitung invers matriknya adalah :

Invers Matriks dengan metode partisi matriks

Contoh :