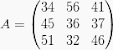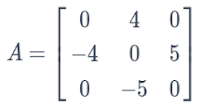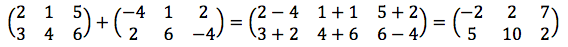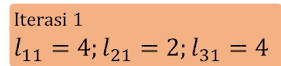Salman Rausyan Fikri: Oktober 2020

بسم الله الرحمن الرحيم

Assalamu'alaykum Warahmatullahi Wabarakatuh

Pada Hari Rabu, 30 September 2020, Kami baru saja menyelesaikan kuliah online bersama Ibu Evy Yosrita S.Si,. M.Kom. di Kelas Aljabar Linear yang membahas Matriks. Tujuan saya membuat artikel di blog ini adalah untuk resume terhadap materi yang sudah dijelaskan oleh Ibu Evy Yosrita. Sebelumnya, penulis ingin memperkenalkan diri :

Nama : Salman Rausyan Fikri

NIM : 202031049

Fakultas Telematika Energi

Program Studi : Teknik Informatika

MATRIKS

Sebelum kita memasuki materi, ada baiknya saya memberikan beberapa poin penting mengenai matriks, di antaranya :

Apa Itu Matriks?
Kegunaan Matriks
Istilah-Istilah Matriks
Jenis-Jenis Matriks
Operasi Matriks

Apa Itu Matriks?

Matriks adalah sekumpulan bilangan yang disusun secara baris atau kolom atau bisa kedua-duanya dan di dalam suatu tanda kurung yang bersifat real, bulat, atau bisa kedua-duanya. Bilangan-bilangan yang membentuk suatu matriks disebut sebagai elemen-elemen matriks.

Kegunaan Matriks

Matriks digunakan untuk menyederhanakan penyampaian data, sehingga mudah untuk diolah. Sebagai contoh : Diketahui jumlah penjualan sepeda jenis A,B dan C dengan harga jual masing-masing 18,30 dan 60 (terhitung dalam juta) pada kota-kota X,Y dan Z, adalah :

Data penjualan sepeda tersebut dapat dibuat dalam bentuk matriks sebagai berikut :

Matriks Harga Jual Sepeda (Juta)

Matriks Jumlah penjualan Tiap Kota

Istilah-Istilah Matriks

Lambang-lambang matriks menggunakan huruf kapital (A,B,C,D,...,Z)
Elemen matriks menggunakan lambang huruf kecil (a,b,c,d,...,z)
Bagian mendatar/horizontal disebut baris
Bagian tegak/vertikal disebut kolom
Indeks "i" menyatakan baris dan indeks "j" menyatakan kolom
Jumlah baris = m dan jumlah kolom = n
Matriks dengan jumlah baris = m dan jumlah kolom = n disebut dengan ukuran (m x n) atau berordo (m x n)
Elemen matrik dapat berupa bilangan bulat, desimal, riil atau kompleks.

Contoh 1

Jumlah baris a = 4 dan jumlah kolom a = 5, maka A berordo 4x5
a32 merupakan elemen baris ke-3 dan kolom ke-2 adalah 0.001
Elemen-elemen diagonal matriks A : 1, π, √3, 1

Contoh 2

Perhatikan jaringan berikut!

aij = 1, jika node i dan j terhubung dan 0, jika node i dan j tidak terhubung

Matriks jaringannya adalah sebagai berikut!

Jenis-Jenis Matriks

Matriks Persegi/Bujur Sangkar ➙ n x n
Matriks Persegi Panjang ➙ m x n
Matriks Segitiga
Matriks Baris ➙ 1 x n
Matriks Kolom ➙ m x 1
Matriks Identitas
Matriks Nol
Matriks Skalar
Matriks Diagonal
Matriks Transpose
Matriks Simetris

1. Matriks Persegi/Bujur Sangkar ➙ n x n

Dikatakan matriks Persegi apabila A memiliki jumlah baris dan kolom yang sama

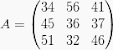
adalah matriks berordo 3

adalah matriks berordo 2

2. Matriks Persegi Panjang ➙ m x n

Tegak/Vertikal apabila m > n

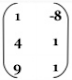
Berordo 3 x 2

Mendatar/Horizontal apabila n > m

Berordo 2 x 3

3. Matriks Segitiga

Matriks Segitiga Atas

Dikatakan matriks segitiga atas apabila angka di bawah diagonal utama pada matriks bujur sangkar adalah nol.

Matriks Segitiga Bawah

Dikatakan matriks segitiga bawah apabila angka di atas diagonal utama pada matriks bujur sangkar adalah nol

Diagonal utama dan diagonal sekunder itu yang mana sih?

4. Matriks Baris ➙ 1 x n

Matriks baris merupakan matriks yang hanya berupa satu baris atau berordo 1 x n

Contoh :

A = (1 3 4 9 6 4 8) berordo 1 x 7
B = (1 3 2) berordo
1 x 3

5. Matriks Kolom ➙ m x 1

Matriks kolom merupakan matriks yang hanya berupa satu kolom atau berordo m x 1

Contoh :

Berordo 3 x 1
B = Berordo 3 x 1

6. Matriks Identitas

Dikatakan Matriks Identitas apabila A adalah matriks bujur sangkar di mana semua elemen kecuali diagonal utama adalah "nol" dan elemen diagonal utama semuanya adalah 1. Matriks identitas diberi lambang "I".

Contoh :

7. Matriks Nol

Dikatakan Matriks Nol karena setiap unsurnya adalah 0, ditulis dengan huruf "O".

Contoh :

8. Matriks Skalar

Dikatakan Matriks Sekalar apabila seluruh unsur-unsur dalam diagonal utama adalah sama dan selainnya adalah nol

Contoh :

9. Matriks Diagonal

Dikatakan Matriks Diagonal apabil A adalah matriks bujur sangkar di mana semua elemen di luar diagonal utama adalah nol dan diagonal utama bukan nol. Matriks Diagonal diberikan lambang berupa "D".

Contoh :

10. Matriks Transpose

Transpose matriks merupakan baris menjadi kolom dan sebaliknya. Jika matriks A ditranspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2 dan begitu seterusnya.

Contoh :

11. Matriks Simetris ➙ A = Aᵀ

Dikatakan Matriks Simetris apabila A adalah matriks bujur sangkar di mana Aᵀ = A

Contoh :

12. Matriks Skew Simetris

Dapat dikatakan Matriks Skew Simetris apabila suatu matriks bujur sangkar ditransposkan akan sama dengan negatif dari matriks semula. Misalkan matriks A adalah matriks bujur sangkar. Agar matriks A dapat dikatakan sebagai Matriks Skew Simetris, maka Transpos A sama dengan -A (Aᵀ = -A). Syarat lainnya adalah semua elemen yang berada di diagonal utama adalah bernilai nol.

Contoh :

Operasi Matriks

Operasi Aritmatik Matriks

Kesamaan (A=B)
Perkalian dengan Skalar kA
Penjumlahan Matriks (A + B)
Pengurangan Matriks (A - B)
Perkalian Matriks (AB = C)

1. Kesamaan (A = B)

Dikatakan Matriks Kesamaan apabila kedua matriks tersebut memiliki ordo dan elemen-elemen yang sama dan bersesuian. Apabila disimbolkan akan menjadi A = B jika a_ij = b_ijuntuk setiap i dan j.

Contoh :

A = B

a - 2 = 1 2b = 4 c = -2

a = 3 b = 2

2. Perkalian dengan Skalar, kA

Perkalian matriks, A=(a_ij) dengan skalar bukan nol K ditulis kA, didefinisikan bahwa setiap elemen A dikalikan dengan konstanta tak nol k, yakni : kA = k(a_ij) = (ka_ij)

Contoh :

3. Penjumlahan (A + B)

Matriks A=(a_ij) dan B=(b_ij) dapat dikatakan penjumlahan apabila A dan B berukuran atau berordo sama. Bilamana A+B=C, maka elemen matrik diberikan : (a_ij) + (b_ij) = (c_ij) Elemen yang seletak dijumlahkan.

Contoh :

A+B=C

Sifat-Sifat Penjumlahan :

A + B = B + A (Sifat Komutatif)
(A + B) + C = A + (B + C) (Sifat Asosiatif)
A + Z = Z + A = A (Z adalah identitas penjumlahan)
A + ( – A) = ( –A) + A = Z (–A merupakan invers penjumlahan dari A)

4. Pengurangan (A - B)

Matriks A=(a_ij) dan B=(b_ij) dapat dikatakan pengurangan apabila A dan B berukuran atau berordo sama. Bilamana A-B=D, maka elemen matrik diberikan : (a_ij) - (b_ij) = (c_ij) Elemen yang seletak dijumlahkan.

A-B=D

5. Perkalian Matriks (AB = C)

Matriks A=[a_ij](m=n) dan B=[b_ij](pxq) dikatakan dapat dikalikan ditulis AB bilamana jumlah kolom A dan jumlah baris B sama. [n=p]

A(mxn)B(pxq) = C(mxq)

Contoh :

Fungsi determinan matriks berupa persegi atau bujur sangkar A dinyatakan dengan det[A] = |A|, didefinisikan sebagai penjumlahan dari hasil kali elementer elemen-elemen yang bertanda "A".

Pada Kasus "n=1", Perhatikan :

A = [a], det(A) = |a| = a

Pada Kasus "n=2"

, maka

det(A) = ad - bc

Pada Kasus "n=3", Menggunakan Metode Sarrus

dengan menggunakan metode Sarrus, det(A) = |A|

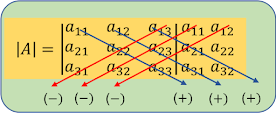
Metode Ekspansi Laplace

A adalah matriks persegi atau bujur sangkar berordo (nxn)

Minor elemen matriks A baris ke-i dan kolom ke-j (a-ij) ditulis Mij diartikan sebagai determinan matriks yang berordo (n-1)x(n-1) yang diperoleh dari A dengan cara menghilangkan baris ke-i dan kolom ke-j.
Kofaktor elemen matriks A merupakan baris ke-i dan kolom ke-j ditulis C-ij didefinisikan sebagai :

Contoh :

Contoh Minor :

Teman-teman bisa cek video saya mengenai pembelajaran matriks, berikut saya sertakan berupa link :

Metode Chio

Andaikan, A=[a_ij](nxn), dan (a₁₁)≠0, maka :

Rumus metode Chio dikenal juga dengan rumus mereduksi ordo atau ukuran matriks. Reduksi ordonya dapat juga menggunakan elemen matriks yang lain, tidak harus menggunakan a₁₁.

Contoh

Hitunglah Det.A dari :